# Cây phân đoạn (Segment Tree)

Quay lại với bài toán ở phần bảng thưa:

Cho một mảng a có n phần tử và q truy vấn có dạng (l, r). Với mỗi truy vấn, tìm và in ra giá trị nhỏ nhất (GTNN) của các phần tử trong khoảng [l, r].

Mảng a ví dụ:

a = [5, 2, 7, 8, 3, 1, 4, 6]

Nếu như các truy vấn chỉ yêu cầu ta tìm GTNN của các đoạn thì bảng thưa là một lựa chọn phù hợp để giải quyết bài toán. Tuy nhiên nếu bài toán có thêm các truy vấn yêu cầu thay đổi giá trị của các phần tử trong mảng, thì ta cần phải cập nhật phần tử và xây dựng lại bảng thưa, khiến cho bảng thưa không còn hiệu quả.

Ta sẽ nói về CTDL Cây phân đoạn (Segment Tree) - một CTDL linh hoạt giúp giải quyết bài toán này.

Giả sử bạn muốn đo chiều cao của tất cả học sinh trong một khu vực.

Một điều chắc chắn là ta không thể đến và đo chiều cao của tất cả học sinh trong khu vực ấy được - nó tốn quả nhiều thời gian và không hề hiệu quả. Thay vì thế, ta có thể bàn giao công việc này cho các trường trong khu vực, mỗi trường đó lại để giáo viên chủ nhiệm đo chiều cao của các em học sinh trong lớp và báo cáo lại để nhà trường tổng hợp lại.

Khi này, thay vì kiểm tra tất cả học sinh ấy thì ta chỉ cần thu thập thông tin tổng hợp từ các trường. Điều này giúp ta thu thập thông tin nhanh hơn và hiệu quả hơn.

Đây chính là ý tưởng chính cho CTDL Segment Tree: Chia một không gian quản lí lớn thành các không gian quản lí nhỏ hơn - một giải pháp chia để trị.

Segment tree là một cây, chính xác hơn là một cây nhị phân đầy đủ - mỗi đỉnh hoặc là một đỉnh lá hoặc có hai đỉnh con. Ta sẽ lưu segment tree trên một mảng st với chỉ số 1 đại diện cho gốc của cây. Với mỗi chỉ số p, 2 \times p và 2 \times p + 1 là hai chỉ số của hai đỉnh con của nó.

Mỗi đỉnh của cây sẽ lưu thông tin về một phân đoạn trên mảng a. Gốc của Segment Tree tượng trưng cho đoạn [1, n]. Với mỗi đỉnh p lưu thông tin về đoạn [l, r]. Nếu p không phải là đỉnh lá thì hai đỉnh con 2 \times p và 2 \times p + 1 sẽ lần lượt lưu thông tin của hai đoạn [l, \left\lfloor (l + r) / 2 \right\rfloor] và [\left\lfloor(l + r) / 2\right\rfloor + 1, r]. Nếu p là đỉnh lá thì nó chỉ quản lý đúng một phần tử duy nhất trên mảng a có chỉ số l = r.

Để xây dựng segment tree, ta có hàm đệ quy build(p, l, r).

Hàm build(p, l, r) của ta hoạt động như sau:

• Nếu l = r, giá trị nhỏ nhất của đoạn [l, r] chính là phần tử a[l]: st[p] = a[l].
• Nếu l \neq r, ta sẽ tính một cách đệ quy GTNN của hai đỉnh con và tính giá trị của đỉnh p từ giá trị của hai đỉnh con: st[p] = min(st[p \times 2], st[p \times 2 + 1]).

void build(int p, int l, int r){
	if(l == r){
		// Đỉnh lá
		st[p] = a[l];
		return;
	}

	int mid = (l + r) >> 1;
	// Tính giá trị hai đỉnh con
	build(p << 1, l, mid);
	build(p << 1 | 1, mid + 1, r);
	
	// Tính giá trị từ hai đỉnh con
	st[p] = min(st[p << 1], st[d << 1 | 1]);
}

Ta xây dựng segment tree bằng cách gọi build(1, 1, n).

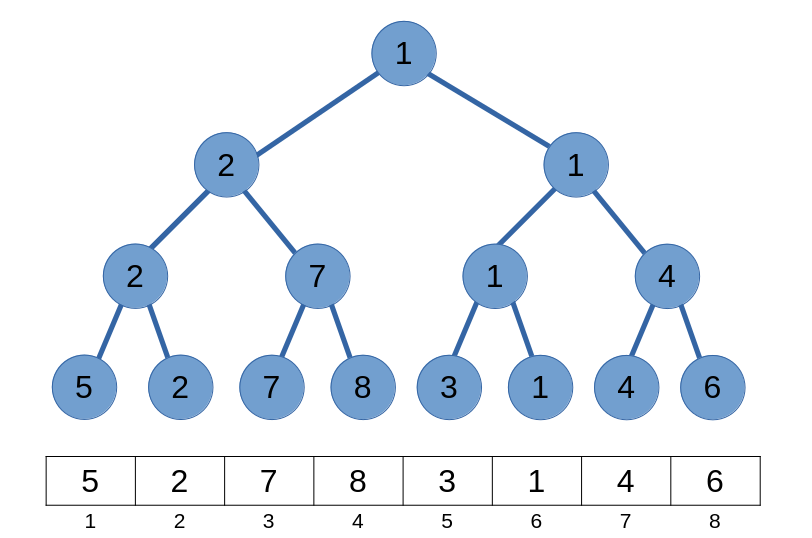
Ta có thể thấy số lượng đỉnh cần tính sẽ là độ phức tạp của việc xây dựng segment tree. Ta có thể tính được số lượng đỉnh trong segment tree sẽ không vượt quá 4n, nên độ phức tạp thuật toán và không gian sẽ bằng O(4n) \approx O(n).

Ta xử lí các truy vấn yêu cầu ta tìm GTNN của một đoạn [l, r] bằng cách sử dụng các đoạn đã được tính trước.

Giả sử ta đang ở đỉnh p lưu GTNN của đoạn [u, v], ta sẽ tính kết quả như sau:

• Nếu [u, v] nằm hoàn toàn bên trong [l, r] (l \le u \le v \le r), ta trả về GTNN lưu trong đỉnh p.
• Nếu [u, v] nằm hoàn toàn bên ngoài [l, r] (v < l hoặc r < u), ta bỏ qua GTNN lưu trong p.
• Nếu một phần [u, v] nằm bên trong [l, r], ta sẽ tính được GTNN từ hai đỉnh con bằng cách áp dụng các bước ở trên và kết hợp GTNN trả về từ hai đỉnh ấy.

Ta tính GTNN của đoạn [l, r] bằng việc xuất phát từ đỉnh 1 và thực hiện các bước ở trên

Hình dưới đây minh họa thao tác trả lời truy vấn tìm GTNN của đoạn [3, 7].

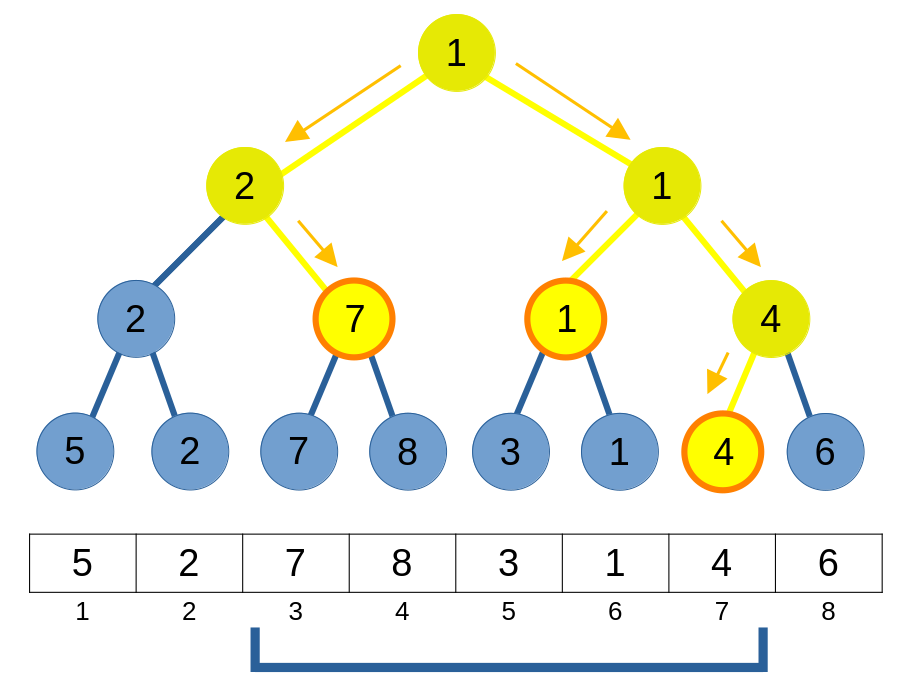
Sau khi thực hiện tìm GTNN, thuật toán của ta trả về GTNN của các đoạn [3, 4], [5, 6] và [7, 7] có GTNN lần lượt là 7, 1 và 4. Kết hợp các kết quả này lại và ta có kết quả của đoạn [3, 7] bằng min([3, 7]) = min([3, 4], [5, 6], [7, 7]) = min(7, 1, 4) = 1.

int ans(int id, int l, int r, int u, int v){
	if(v < l || r < u) return INT_MAX; // Trả về giá trị không làm ảnh hưởng kết quả
	if(u <= l && r <= v) return st[id];
	int mid = (l + r) >> 1;
	return min(ans(id << 1, l, mid, u, v), ans(id << 1 | 1, mid + 1, r, u, v));
}

Để tìm GTNN của phân đoạn [l, r], ta gọi ans(1, 1, n, l, r).

Độ phức tạp thuật toán sẽ là O(\log{n}).

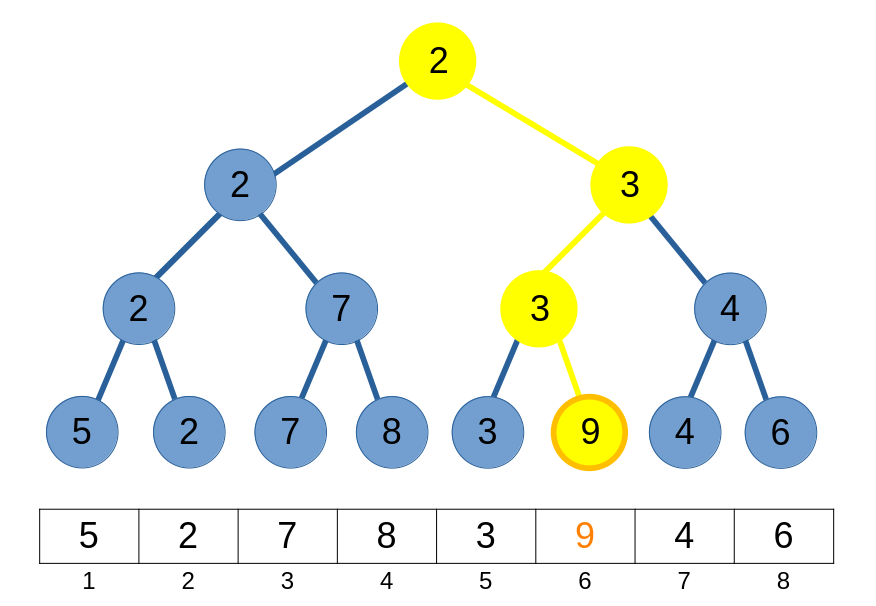
Đối với các truy vấn yêu cầu ta thay đổi giá trị của một phần tử trong mảng, ta cập nhật phần tử ấy và tính toán lại các phân đoạn phụ thuộc vào phần tử đó.

// u: chỉ số phần tử cần cập nhật
// v: giá trị cập nhật
void update(int id, int l, int r, int u, int v){
	if(l == r){
		st[id] = v;
		return;
	}
	int mid = (l + r) >> 1;
	if(u <= mid) update(id << 1, l, mid, u, v);
	else update(id << 1 | 1, mid + 1, r, u, v);
	st[id] = min(st[id << 1], st[id << 1 | 1]);
}

Để cập nhật giá trị của phần tử thứ i thành x , ta gọi update(1, 1, n, i, x).

Thuật toán của ta sẽ đi qua số lượng đỉnh bằng với chiều cao của cây nên có độ phức tạp O(\log{n}).

Đối với cập nhật đoạn, ta cần một cách xử lí thông minh hơn.

Giả sử ta áp dụng cách cập nhật đoạn tương tự cách làm với cập nhật điểm, số lượng phân đoạn ta cần cập nhật có thể lên đến O(n).

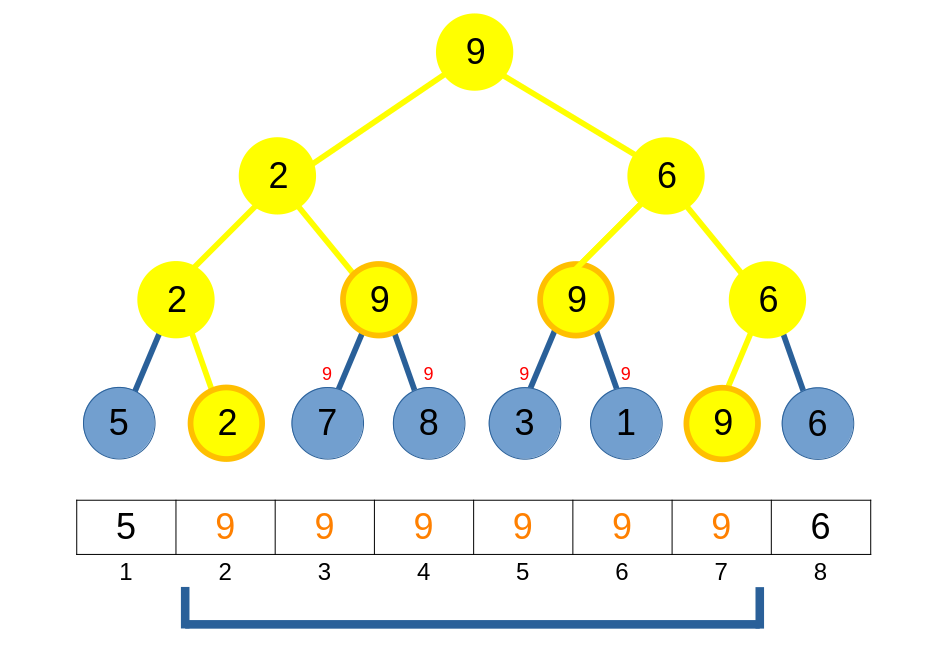
Nếu ta cập nhật: "thay đổi các phần tử trong khoảng [2, 7] thành 9":

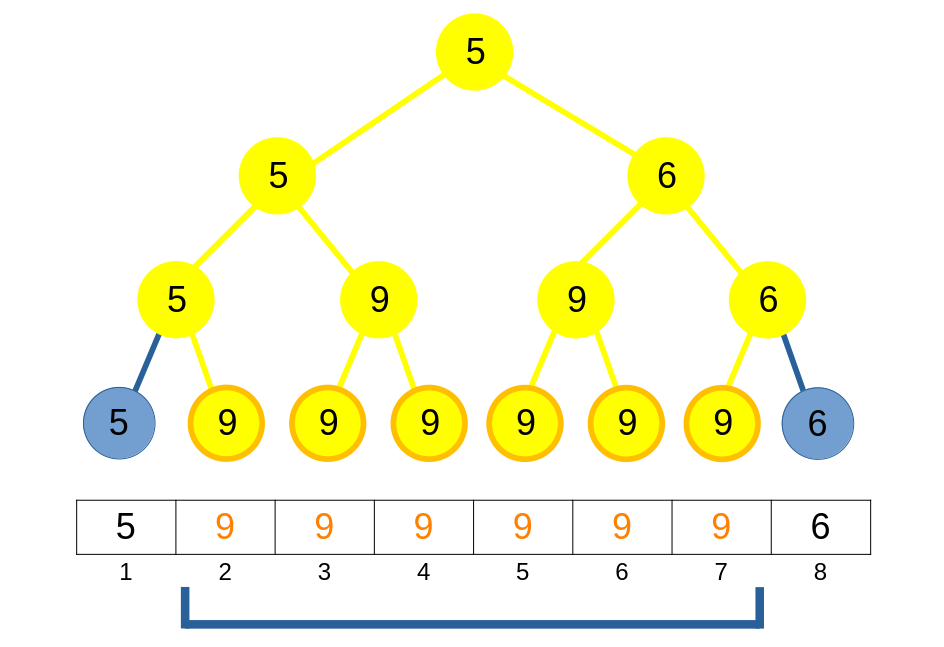
Có thể thấy thao tác cập nhật O(n) này thì sẽ không hề hiệu quả. Vậy làm sao để khắc phục nhược điểm này?

Cập nhật lười, hay lazy propagation, là một kĩ thuật giúp ta thực hiện truy vấn cập nhật đoạn hiệu quả trên segment tree.

Giả sử ta thực hiện cập nhật phân đoạn trên một đỉnh, ta sẽ lưu cập nhật này và không cập nhật đỉnh ấy.

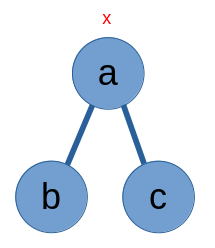
Chỉ khi đỉnh này được xét đến thì ta mới thực hiện cập nhật giá trị trên đỉnh ấy mà ta đã lưu. Sau khi cập nhật xong thì ta lưu cập nhật lên các đỉnh con và xóa thông tin cập nhật trên đỉnh này.

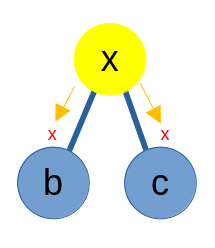
Bằng cách này, ta có thể giảm số lượng đỉnh mà ta cần đến khi cập nhật.

void lazy(int id, int l, int r){
	// nếu đỉnh id không lưu bất kì truy vấn cập nhật nào
	if(lz[id] == -1) return;
	st[id] = lz[id];
	if(l != r) { // nếu đỉnh id không phải đỉnh lá
		lz[id << 1] = lz[id << 1 | 1] = lz[id];
	}
	lz[id] = -1;
}
// cập nhật các phần tử khoảng [u, v] thành x
void update(int id, int l, int r, int u, int v, int x){
	lazy(id, l, r);
	if(v < l || r < u) return;
	if(u <= l && r <= v){
		lz[id] = x;
		lazy(id, l, r);
		return;
	}
	int mid = (l + r) >> 1;
	update(id << 1, l, mid, u, v, x);
	update(id << 1 | 1, mid + 1, r, u, v, x);
	st[id] = min(st[id << 1], st[id << 1 | 1]);
}

Để cập nhật giá trị của các phần tử từ l đến r thành x , ta gọi update(1, 1, n, l, r, x).

Độ phức tạp của truy vấn cập nhật đoạn giờ đây giảm xuống còn O(\log{n}).

Ta cũng cần sửa lại hàm ans khi áp dụng cập nhật lười.

int ans(int id, int l, int r, int u, int v){
	lazy(id, l, r);
	if(v < l || r < u) return INT_MAX;
	if(u <= l && r <= v) return st[id];
	int mid = (l + r) >> 1;
	return min(ans(id << 1, l, mid, u, v), ans(id << 1 | 1, mid + 1, r, u, v));
}

Độ phức tạp của hàm ans không thay đổi: O(\log{n}).