# Ứng dụng của thuật toán tìm kiếm

Hai thuật toán tìm kiếm trên đồ thị đã được nói ở phần trước tuy đơn giản nhưng lại có tính ứng dụng rất cao. Ta sẽ điểm qua một số ứng dụng của nó.

# Xây dựng cây khung của đồ thị

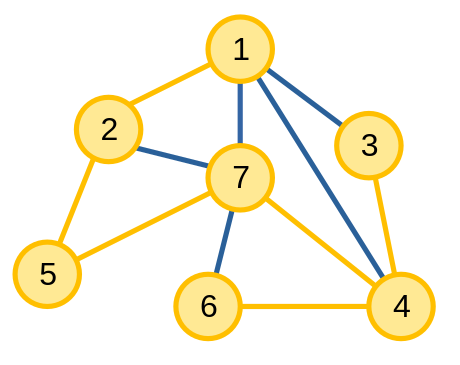
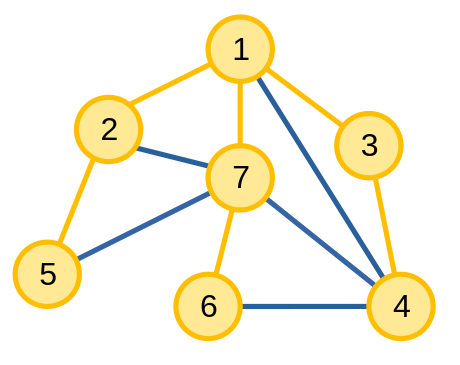
Ta có một đồ thị G = (V, E). Nếu ta có một đồ thị G' = G và loại bỏ một số cạnh của G' sao cho G' là một cây và các đỉnh vẫn liên thông thì đồ thị G' được gọi là cây khung của G.

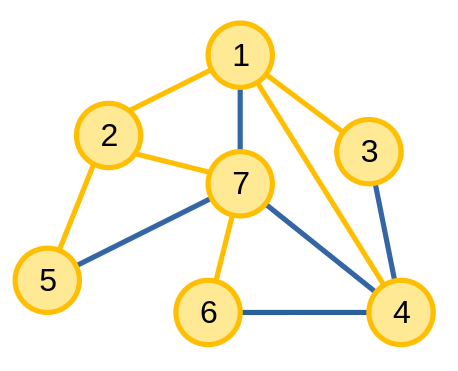
Các cạnh màu cam là các cạnh thuộc cây khung của đồ thị. Có thể có nhiều hơn một cây khung.

Để xây dựng cây khung từ các thuật toán kìm kiếm, ta làm theo cách sau: khi thuật toán DFS hoặc BFS di chuyển từ đỉnh u sang đỉnh v, ta thêm cạnh uv vào cây khung. Ta sẽ gọi cây khung tạo nên từ DFS và BFS lần lượt là cây DFS và cây BFS.


Cây DFS có gốc là 1	Cây BFS có gốc là 1

# Tìm thành phần liên thông

Có thể dễ dàng nhận thấy rằng khi ta thực hiện DFS hoặc BFS một đỉnh s bất kì trên một đồ thị vô hướng, hai thuật toán này sẽ đi đến những đỉnh liên thông với s. Từ đấy ta tìm ra được một thành phần liên thông trên đồ thị, với các đỉnh là đỉnh s và các đỉnh liên thông với nó.

int cc = 0;
for(int i = 1; i <= n; ++i){
	if(vst[i] == 0) {
		// bfs(i);
		dfs(i);
		++cc;
	}
}
cout << cc; // cc là số TPLT trong đồ thị

# Flood fill

Trong nhiều phần mềm vẽ, tồn tại công cụ có tên gọi bucket giúp ta tô màu một vùng có màu sắc giống nhau thành màu ta chọn.

Thuật toán giúp công cụ này thành hiện thực có tên gọi là thuật toán flood fill.

Thuật toán flood fill được sử dụng trên mặt phẳng 2 chiều. Xuất phát từ điểm (x, y), thuật toán sẽ đi đến các đỉnh có chung tính chất với đỉnh này. Ta xuất phát từ một đỉnh sang 4 phía (Đông/Tây/Nam/Bắc) hoặc 8 phía (Đông/Tây/Nam/Bắc/Đông Nam/Đông Bắc/Tây Nam/Tây Bắc) của đỉnh.

Đoạn code ví dụ dưới đây là một thuật toán flood fill sẽ tìm trên mặt phẳng 2 chiều kích thước n \times m những vùng có giá trị 0.

//                 D   T  N   B DN  DB  TN  TB
static int dx[] = {0,  0, 1, -1, 1, -1,  1, -1};
static int dx[] = {1, -1, 0,  0, 1,  1, -1, -1};
int mat[N][M];
bool vst[N][M];
int n, m;

void floodfill(int x, int y){
	// Kiểm tra nếu điểm nằm ngoài mặt phẳng
	if(x < 1 || x > n || y < 1 || y > m) return; 
	// Kiểm tra điểm có giá trị 0 hay không 
	if(mat[x][y] != 0) return;
	// Kiểm tra nếu đã thăm điểm rồi
	if(vst[x][y]) return;

	vst[x][y] = 1;
	// Đổi thành 8 nếu được di chuyên sang 8 hướng
	for(int i = 0; i < 4; ++i){
		floodfill(x + dx[i], y + dy[i]);
	}
}

void find_region(){
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j <= m; ++j){
			floodfill(i, j);
		}
	}
}

# Tìm đường đi ngắn nhất trên đồ thị

BFS có thể tìm đường đi ngắn nhất từ một đỉnh s đến các đỉnh khác trên đồ thị, nếu định nghĩa khoảng cách từ một đỉnh u đến một đỉnh v là số cạnh mà nó cần đi qua.

int dist[N];
void bfs(int s){
	queue<int> q;
	q.push(s);
	dist[s] = 0;
	vst[s] = 1;

	while(q.size() > 0) {
		int u = q.front(); q.pop();		
		for(int v : adj[u]){
			if(vst[v]) continue;
			dist[v] = dist[u] + 1;
			q.push(v);
		}
	}
}

# Kiểm tra đồ thị hai phía

Ta có thể xác định nếu đồ thị của ta là đồ thị hai phía hay không bằng cách tìm chu trình có lẻ đỉnh trong đồ thị.

Ta chỉnh sửa đoạn code ở phần trên như sau: sau khi xác định đường đi ngắn nhất, ta các cặp cạnh uv: nếu khoảng cách của hai đỉnh u, v không đồng chằn hoặc đồng lẻ thì đồ thị không phải đồ thị hai phía. Nếu điều này không xảy ra thì đồ thị của ta là đồ thị hai phía.

Vì chỉ quan tâm tính chẵn lẻ nên ta có thể thay đổi dist lưu tính chẵn lẻ của đường đi ngắn nhất từ đỉnh s.

bool dist[N];
bool bipartite(int s){
	queue<int> q;
	q.push(s);
	dist[s] = 0;
	vst[s] = 1;

	while(q.size() > 0) {
		int u = q.front(); q.pop();		
		for(int v : adj[u]){
			if(vst[v]) {
				if(dist[u] != dist[v]) return 0;
				continue;
			}
			dist[v] = dist[u] ^ 1;
			q.push(v);
		}
	}
	return 1;
}
bool is_bipartite(){
	for(int i = 1; i <= n; ++i){
		if(vst[i]) continue;
		if(!bipartite(i)) return 0;
	}	
	return 1;
}

Mặc dù DFS không thể tính đường đi ngắn nhất, ta vẫn có thể xác định tính hai phía của đồ thị bằng DFS.

Ta có dist[u] là tính chắn lẻ của một đường đi từ s đến u. Sau đó, ta xét trường hợp giống ở trên.

bool bipartite(int u){
	vst[u] = 1;
	for(int v : adj[u]){
		if(vst[v]) {
			if(dist[u] != dist[v]) return 0;
			continue;
		}
		dist[v] = dist[u] ^ 1;
		bipartite(v);
	}
	return 1;
}

# Sắp xếp Tô-pô

Thứ tự tô-pô (Topological Ordering) của một đồ thị có hướng G = (V, E) là thứ tự sắp xếp của các đỉnh trên một đoạn thẳng sao cho với mỗi cạnh uv, đỉnh u đứng trước đỉnh v trong thứ tự sắp xếp.

Ta có thể tìm thứ tự tô-pô của một DAG bằng DFS hoặc thuật toán Kahn.

Xem chi tiết tại phần thuật toán sắp xếp Tô-pô.

# Phát hiện chu trình

Đối với đồ thị vô hướng, việc xác định sự tồn tại của chu trình khá đơn giản: đồ thị không có chu trình nếu nó là một cây. Nếu không phải cây thì đồ thị chắc chắn có chu trình.

Đối với đồ thị có hướng, ta sẽ giải quyết theo hướng khác bằng DFS.

Trong quá trình đỉnh u của DFS, ta sẽ chia ra làm 3 giai đoạn:

Giai đoạn 1: Chưa được duyệt. Ở giai đoạn này, đỉnh u chưa được xử lí khi DFS đang chạy.
Giai đoạn 2: Đang được xét đến. Ở giai đoạn này, đỉnh u đã được DFS duyệt qua nhưng chưa duyệt xong.
Giai đoạn 3: Đã được xét đến. Ở giai đoạn này, đỉnh u đã được DFS duyệt qua và đã duyệt xong.

Từ 3 giai đoạn này, ta có thể phân loại các cạnh của đồ thị trong quá trình duyệt tạo cây DFS thành các cạnh sau:

Cạnh cây (Tree Edge): đây là cạnh của cây DFS. Khi ta đi từ đỉnh u sang đỉnh v thì cạnh uv là cạnh cây khi đỉnh u ở giai đoạn 2 và đỉnh v ở giai đoạn 1.
Cạnh ngược/hai phía (Back/Bidirectional Edge): đây là cạnh không thuộc cây DFS. Khi ta đi từ đỉnh u sang đỉnh v thì cạnh uv là cạnh ngược khi đỉnh u ở giai đoạn 2 và đỉnh v ở giai đoạn 2. Cạnh ngược giúp ta biết được đỉnh v là tổ tiên của đỉnh u trên cây DFS. Nếu v là cha của đỉnh u thì cạnh của ta là cạnh hai phía.
Cạnh xuôi/chéo (Forward/Cross Edge): đây là cạnh không thuộc cây DFS. Khi ta đi từ đỉnh u sang đỉnh v thì cạnh uv là cạnh xuôi/chéo khi đỉnh u ở giai đoạn 2 và đỉnh v ở giai đoạn 3. Điểm khác nhau giữa cạnh xuôi và cạnh chéo là cạnh xuôi sẽ chỉ một đỉnh đến một đỉnh hậu duệ của nó còn cạnh chéo thì không.

Ta sẽ tìm được chu trình nếu cây DFS tồn tại cạnh ngược trên đồ thị. Chu trình hai đỉnh cũng có thể tồn tại nếu tồn tại cạnh hai phía.

int vst[N];
// vst[i] = 0: giai đoạn 1

// p là cha của đỉnh u
// nếu u là đỉnh gốc thì p = 0

void dfs(int u, int p){
	vst[u] = 1; // giai đoạn 2
	for(int v : adj[u]){
		if(vst[v] == 0){
			// cạnh cây
			dfs(v, u);
		} else if (vst[v] == 1) {
			if(v == p); // cạnh hai phía
			else; // cạnh ngược
		} else if (vst[v] == 2) {
			// cạnh xuôi/chéo
		}
	}
	vst[u] = 2; // giai đoạn 3
}

Ở hình ví dụ dưới đây, ta có cây DFS gốc là 1, cạnh màu cam là cạnh cây, cạnh màu đỏ là cạnh ngược, cạnh màu lục là cạnh chéo còn cạnh màu lam là cạnh xuôi.

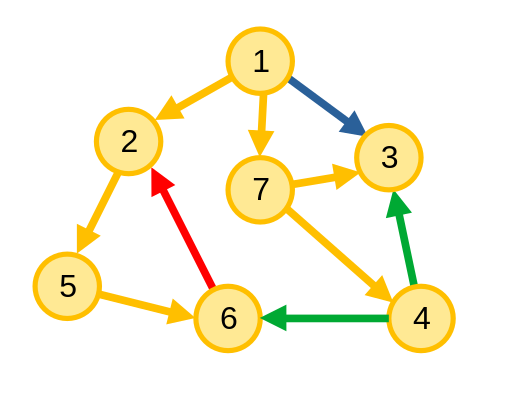
# Tìm khớp, cầu

Bài toán tìm khớp cầu trên đồ thị vô hướng có thể được giải quyết hiệu quả bằng DFS.

Ta sẽ lưu hai thông tin trên cây DFS:

num: thứ tự duyệt đỉnh của DFS.
low: đỉnh có thứ tự duyệt nhỏ nhất có thể đi đến được từ một đỉnh.

Ban đầu, khi bắt đầu duyệt đỉnh u, ta có num[u] = low[u]. Sau đó, trong quá trình duyệt từ đỉnh u, ta cập nhật low[u] thành giá trị nhỏ nhất giữa low[u] và low của các đỉnh nằm trong cây con gốc u trong cây DFS, và num của các đỉnh v được nối với u bởi cạnh ngược.

Từ những thông tin này, ta có thể xác định khớp cầu trên đồ thị.

Một đỉnh u là đỉnh khớp khi tồn tại một đỉnh con trên cây DFS v sao cho low[v] \ge num[u]. Nếu low[v] \lt num[u] thì v có thể đến được một đỉnh có num nhỏ hơn num[u] bằng cạnh ngược. Nếu điều này không xảy ra, thì để v có thể đi sang các đỉnh khác ngoài các đỉnh trong cây DFS con gốc v, ta cần phải đi qua đỉnh u, và khi xóa đỉnh u đi thì v không thể đi đến các đỉnh ấy \rightarrow đỉnh u là đỉnh khớp.

Một trường hợp nữa của đỉnh khớp là khi đỉnh gốc của cây DFS có ít nhất 2 đỉnh con thì đỉnh gốc cũng là đỉnh khớp.

Một cạnh uv là cạnh cầu khi low[v] \gt num[u] với cách giải thích tương tự với đỉnh khớp.

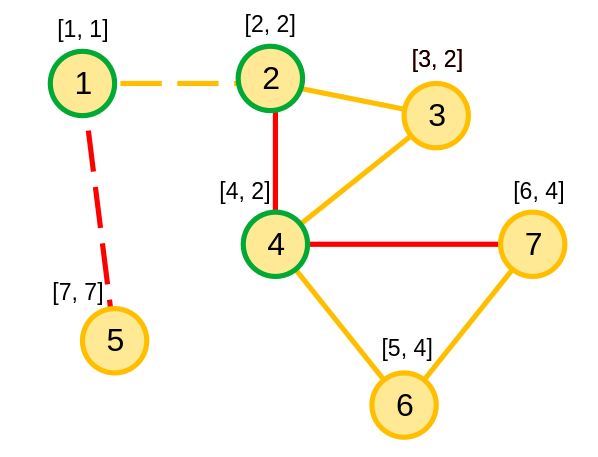
Ở hình trên, ta có đồ thị DFS sau khi duyệt đồ thị:

Số bên phải chỉ low của đỉnh v.
Số bên trái chỉ num của đỉnh u.
Cạnh vàng chỉ các cạnh cây thuộc cây DFS.
Cạnh đỏ chỉ các cạnh ngược không thuộc cây DFS.
Các đỉnh viền xanh chỉ các đỉnh khớp.
Các cạnh nét dứt chỉ các cạnh cầu.

int num[N], low[N], tdfs = 0; // tdfs: số đỉnh đã duyệt
void dfs(int u, int p){
	num[u] = low[u] = ++tdfs;
	int nc = 0;
	bool khop = 0;
	for(int v : adj[u]){
		if(num[v] == 0){
			dfs(v, u);
			++nc;
			low[u] = min(low[u], low[v]);
			khop |= (p != 0 && low[v] >= num[u]) || (p == 0 && nc == 2);
			if(low[v] > num[u]); // uv là cạnh cầu
		} else if(v != p) low[u] = min(low[u], num[v]);
	}
	if(khop); // u là đỉnh khớp
}

# Tìm thành phần liên thông mạnh

Có thể sử dụng hai thuật toán tìm TPLT mạnh trên đồ thị có hướng chính là thuật toán của Kosaraju và thuật toán của Tarjan.

# Thuật toán Kosaraju

Thuật toán Kosaraju là một thuật toán tìm TPLT mạnh khá đơn giản.

Ta sẽ thực hiện DFS trên đồ thị. Sau mỗi lần duyệt xong một đỉnh u, ta thêm đỉnh u vào một danh sách theo thứ tự ngược lại (nếu đỉnh u được duyệt đầu tiên thì nó sẽ ở cuối danh sách,...).

Sau đó, đảo ngược các cạnh trên đồ thị (cung uv đổi thành cung vu) và thực hiện DFS theo thứ tự các đỉnh có trong danh sách.

Số lần ta thực hiện DFS sẽ là số TPLT mạnh trong đồ thị và các đỉnh mà DFS duyệt đến với mỗi lần gọi là các đỉnh cùng thuộc 1 TPLT mạnh.

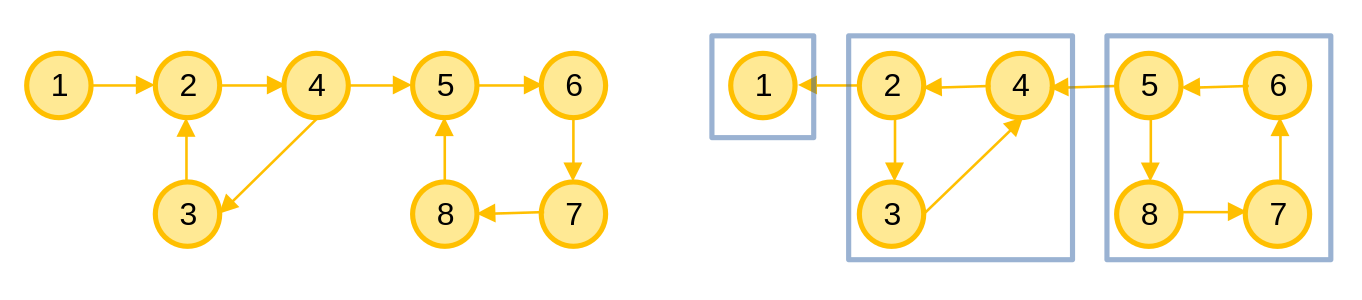
// Đồ thị với các đỉnh bị đảo ngược
vector<int> rev[N];

bitset<N> vst;
vector<int> arr;

// Chỉ số của TPLT chứa u
int inCC[N], cc = 0;

void dfs1(int u){
	vst[u] = 1;
	arr.push_back(u);
	for(int v : adj[u]){
		if(vst[v]) continue;
		dfs1(v);
	}
}

void dfs2(int u){
	inCC[u] = cc;
	for(int v : rev[u]){
		if(inCC[v]) continue;
		dfs2(v);
	}
}

void scc(){
	for(int i = 1; i <= n; ++i){
		if(vst[u] == 0) dfs1(u);
	}
	for(int i = n; i >= 1; --i){
		if(inCC[arr[i - 1]] == 0) {
			dfs2(arr[i - 1]);
			++cc;
		}
	}
	cout << cc; // Số TPLT mạnh
}

# Thuật toán của Tarjan

Thuật toán của Tarjan là một thuật toán tìm kiếm TPLT mạnh.

Ta sẽ sử dụng num và low giống như phần khớp cầu, tuy nhiên việc cập nhật low sẽ có chút khác biệt. Ta chỉ cập nhât low[u] bằng low[v] nếu ta chưa xác định được v thuộc TPLT mạnh nào.

Ta có thuật toán DFS duyệt như sau:

Khi ta bắt đầu duyệt đỉnh u, ta thêm u vào một stack. Sau khi kết thúc việc duyệt các phần tử kề đỉnh u, nếu num[u] = low[u] thì ta đã tìm được một TPLT, với các đỉnh là những đỉnh nằm trên đỉnh u trong stack. Ta đánh đấu và loại các đỉnh này ra khỏi stack, tiếp tục duyệt các đỉnh khác.

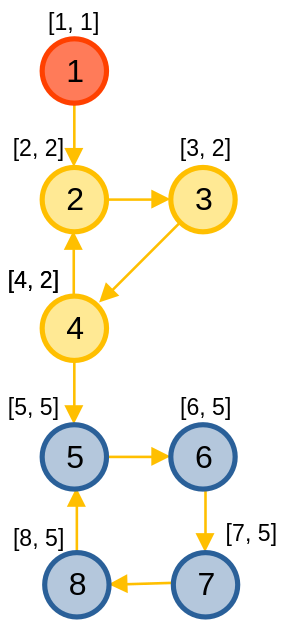
Những đỉnh có cùng màu sắc trong hình là các đỉnh thuộc cùng một TPLT.

int num[N], low[N], tdfs = 0;
int inCC[N], cc = 0;
stack<int> st;

void dfs(int u){
    num[u] = low[u] = ++tdfs;
    vst[u] = 1;
    st.push(u);
    for(int v : adj[u]){
        if(num[v] == 0) dfs(v);
        if(inCC[v] == 0) low[u] = min(low[u], low[v]);
    }
    if(num[u] == low[u]){
        ++cc;
        while(true){
            int v = st.top(); st.pop();
            inCC[v] = cc;
            if(u == v) break;
        }
    }
}

void scc(){
	for(int i = 1; i <= n; ++i){
		if(inCC[u] == 0) dfs(u);
	}
	cout << cc; 
}

thuật toán đồ thị lý thuyết đồ thị ứng dụng của thuật toán tìm kiếm competitive programming cp