# Lí thuyết đồ thị

Hình ảnh dưới đây là một ví dụ về một đồ thị:

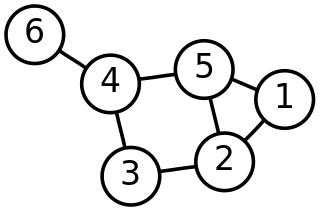
Những vòng tròn được gọi là các đỉnh (vertices) hoặc các nút (nodes), và những đường thẳng nối những vòng tròn được gọi là các cạnh (edges).

Về cơ bản, đồ thị là một tập hợp hữu hạn gồm các đỉnh và được nối với nhau bởi các cạnh.

Một đồ thị G sẽ được kí hiệu: G = (V, E)

Với V là tập hợp chứa các đỉnh, và E là tập hợp chứa các cạnh, mỗi cạnh có dạng một cặp giá trị {u, v} (có thể được viết thành uv). Ví dụ:

G = {1, 2, 3, 4, 5, 6}, {1, 2}, {1, 5}, {2, 5}, {2, 3}, {3, 4}, {4, 5}, {4, 6}

chính là đồ thị ở hình ví dụ trên.

Tập hợp đỉnh V của đồ thị G được kí hiệu V(G), tập hợp cạnh được kí hiệu E(G).

Các dạng đồ thị được nói đến dưới đây là một số dạng đồ thị phổ biến trong lập trình thi đấu.

Một đồ thị không có khuyên, không có các cạnh song song, vô hướng và không có trọng số được gọi là đơn đồ thị (hay chỉ đơn giản là đồ thị).

Note:

• Khuyên là các cạnh có dạng uu.
• Hai hoặc nhiều cạnh song song với nhau khi các cạnh có chung hai điểm đầu mút.

Một đồ thị tồn tại các cạnh song song được gọi là đa đồ thị.

Đơn đồ thị là một dạng đặc biệt của đa đồ thị.

Một đồ thị là vô hướng (undirected) khi cạnh không được chỉ định hướng. Nếu đồ thị tồn tại một cạnh uv, ta có thể đi theo hướng u \rightarrow v và hướng v \rightarrow u. Khi này, việc viết 2 cạnh uv và vu là như nhau và ta chỉ cần viết 1 trong 2 cạnh.

Một đồ thị là có hướng (directed) khi cạnh được chỉ định hướng. Điều này có nghĩa rằng nếu đồ thị tồn tại một cạnh uv, ta chỉ có thể đi theo hướng u \rightarrow v. Khi này, 2 cạnh uv và vu phân biệt.

Ta có thể gọi các cạnh trong đồ thị có hướng là cung (arc).

Một đồ thị có trọng số (weighted) là một đồ thị có các cạnh được gán một giá trị. Các giá trị có thể tượng trưng cho khoảng cách, chi phí di chuyển,...

Một đồ thị không có trọng số (unweighted) là một đồ thị các cạnh không được gán giá trị. Có thể nhìn dạng đồ thị này theo cách khác rằng đồ thị không trọng số là một đồ thị có trọng số với các cạnh được gán giá trị bằng nhau (Ví dụ như có trọng số bằng 1).

Một đồ thị G_s = (V, E) là đồ thị con (subgraph) của một đồ thị G = (V, E) khi tập đỉnh và tập cạnh của G_s là tập con của các tập hợp tương ứng của G, hay $V(G_s) \subseteq V(G) $ và $E(G_s) \subseteq E(G) $ thỏa mãn.

Một số dạng đồ thị đặc biệt ta cần biết.

Một đồ thị là đầy đủ khi tất cả các cặp đỉnh của đồ thị được nối với nhau bởi một cạnh.

Nếu một đồ thị G có |V| đỉnh vừa vô hướng vừa đầy đủ, số cạnh của G sẽ là |E| = \frac{|V| \times (|V| - 1)}{2}.

Một đồ thị là hai phía (bipartite) khi tập đỉnh của nó có thể chia làm hai tập X và Y rời nhau sao cho không cặp đỉnh nào nối với nhau với mỗi tập.

DAG là một đồ thị có hướng không có chu trình . Một đồ thị có hướng được gọi là một DAG khi và chỉ khi đồ thị tồn tại thứ tự tô pô.

Một đồ thị được gọi là một cây khi nó là một đồ thị vô hướng, liên thông và không có chu trình.

Ta cùng điểm qua một số khái niệm, tính chất liên quan đến đồ thị.

Cho một đồ thị G = (V, E):

1. Hai đỉnh u và v của G kề nhau (adjacent) khi uv \in E, hay uv là một cạnh của G. Khi này, ta nói cạnh uv là cạnh liên thuộc (incident) với hai đỉnh u và v, đồng thời u, v là hai đỉnh đầu mút (endpoints) của cạnh uv.

2. Cho đỉnh u \in V, các đỉnh hàng xóm (neighbours) với đỉnh u là tất cả các đỉnh v \in V thỏa mãn uv \in E, hay tất cả các đỉnh v kề với u.

3. Cho đỉnh u \in V, bậc (degree) của đỉnh u chính là số lượng hàng xóm của đỉnh u. Kí hiệu: deg(u). Ta có một số bổ đề về bậc như bổ đề bắt tay: \sum_{u \in V} deg(u) = 2|E| Nếu G là một đồ thị có hướng, ta định nghĩa:

• Bán bậc ra (out-degree) của đỉnh u, kí hiệu deg^+(u), là số lượng cạnh xuất phát từ đỉnh u, hay giá trị của |\{v \in V | uv \in E\}|.
• Bán bậc vào (in-degree) của đỉnh u kí hiệu deg^-(u), là số lượng cạnh kết thúc tại đỉnh u, hay giá trị của |\{v \in V | vu \in E\}|.

Trong đồ thị có hướng, tổng bán bậc vào của tất cả các đỉnh luôn bằng tổng bán bậc ra của tất cả các đỉnh (vì mỗi cạnh có một đỉnh bắt đầu và một đỉnh kết thúc).

Cho một đồ thị G = (V, E):

1. Một đường đi (walk) (trong G) là một dãy các đỉnh (v_0, v_1, v_2,..., v_k) thuộc G và các cạnh (v_0v_1, v_1v_2,..., v_{k - 1}v_k) là các cạnh thuộc đồ thị.

Một trail là một đường đi trong đó tất cả các cạnh trên đường đi đôi một phân biệt.

Một path là một đường đi trong đó tất cả các đỉnh trên đường đi đôi một phân biệt (suy ra các cạnh trên đường đi cũng đôi một phân biệt).

2. Với w = (v_0, v_1, v_2,..., v_k) là một đường đi trong G, ta có:

• v_0, v_1, v_2,..., v_k là các đỉnh của w.
• v_0v_1, v_1v_2,..., v_{k - 1}v_k là các cạnh của w.
• Độ dài (khoảng cách) của đường đi w là một số nguyên không âm k (k tương đương với số cạnh trên đường đi, và k + 1 tương đương với số đỉnh). Nếu G có trọng số, độ dài của đường đi là tổng trọng số của các cạnh trên đường đi.
• v_0 được gọi là đỉnh đầu (starting point) của w, ta nói w bắt đầu tại tại đỉnh v_0.
• v_k được gọi là đỉnh cuối (ending point) của w, ta nói w kết thúc tại tại đỉnh v_k.
• Cho hai đỉnh p và q thuộc G, ta nói đường đi từ p đến q là đường đi bắt đầu từ đỉnh p và kết thúc tại đỉnh q.

3. Một đường đi khép kín (closed walk, tour) của G một đường đi mà đỉnh cuối trùng với đỉnh đầu. Hay nói cách khác, là một dãy các đỉnh (v_0, v_1, v_2,..., v_k) với v_0 = v_k.

4. Một chu trình (cycle) của G là một đường đi khép kín (v_0, v_1, v_2,..., v_k) với k \ge 3 và các đỉnh (v_0, v_1, v_2,..., v_{k - 1}) đôi một phân biệt. Một số trường hợp đặc biệt:

• Nếu G là một đồ thị có hướng hoặc là một đa đồ thị, G tồn tại chu trình có 2 đỉnh khi trong đồ thị tồn tại hai đỉnh a và b được nối với nhau bởi 2 cạnh song song. Ví dụ:
• G tồn tại chu trình có 1 đỉnh nếu trong đồ thị tồn tại cạnh khuyên. Ví dụ:

5. Một đường đi (chu trình) là sơ cấp nếu nó không đi qua đỉnh nào hai lần trở lên. Một đường đi (chu trình) là đơn giản nếu nó không đi qua cạnh nào hai lần trở lên.

Cho một đồ thị G = (V, E):

1. Hai đỉnh u và v của G liên thông nếu tồn tại ít nhất 1 đường đi từ u đến v.

2. G liên thông (connected) khi mọi cặp đỉnh của G tồn tại đường đi. G song liên thông (biconnected) nếu nó liên thông và không có đỉnh khớp, nghĩa là nếu xóa một đỉnh bất kì thì đồ thị vẫn liên thông.

3. Đối với một đồ thị có hướng:

• Một đồ thị có hướng G được gọi là liên thông mạnh (strongly connected) nếu mọi cặp đỉnh của G tồn tại đường đi.
• Một đồ thị có hướng G được gọi là liên thông yếu (weakly connected) nếu khi ta xem đồ thị G là một đồ thị vô hướng thì G liên thông.

4. Đỉnh u thuộc G được gọi là khớp (articulation point) nếu khi ta xóa bỏ đỉnh u khỏi đồ thị thì G không còn liên thông.

5. Cạnh uv thuộc G được gọi là cầu (bridge) nếu khi ta xóa bỏ cạnh uv khỏi đồ thị thì G không còn liên thông.

6. Nếu G không liên thông, G sẽ tồn tại nhiều đồ thị con liên thông, rời nhau. Mỗi đồ thị con đó được gọi là một thành phần liên thông (TPLT) (connected component) của G.

Đối với các đồ thị cây, ta có thêm một số định nghĩa và tính chất:

Cho một đồ thị G = (V, E):

1. G là cây khi nó thỏa mãn ít nhất 2 điều kiện dưới đây:

• G không có chu trình
• G liên thông
• Số cạnh bằng số đỉnh trừ 1 hay |E(G)| = |V(G)| - 1

2. G là một rừng cây (forest) khi G có nhiều hơn 1 TPLT, mỗi TPLT là một cây.

3. Chỉ tồn tại một đường đi độc nhất nối 2 đỉnh bất kì trên G.

4. Thêm một cạnh bất kì chưa có trong G sẽ xuất hiện một chu trình.

Đồng thời, việc xóa một cạnh bất kì trong G sẽ làm tăng số TPLT của cây \rightarrow tất cả các cạnh của G đều là cạnh cầu.

Cho một đồ thị cây T = (V, E):

1. Gốc (root) của T là một đỉnh thuộc T được lựa chọn làm gốc. Thông thường, các bài toán đều chọn đỉnh 1 làm gốc của cây, nếu bài toán không chỉ rõ gốc của cây là đỉnh nào, hãy giả sử nó là đỉnh 1. Một số cây có thể không có gốc.

2. Đỉnh lá (leaf) của T là các đỉnh có bậc bằng 1.

3. Nếu T có gốc, các đỉnh thuộc T sẽ hình thành quan hệ cha/con (parent/child). Cụ thể:

• Với mỗi cặp cạnh uv bất kì: nếu khoảng cách tới gốc của v ngắn hơn hơn khoảng cách tới gốc của u, đỉnh v sẽ là cha (parent) của đỉnh u. Nếu khoảng cách tới gốc của v dài hơn thì đỉnh v sẽ là con (child) của đỉnh u.
• Một đỉnh có thể có nhiều con, nhưng chỉ có một cha.
• Đỉnh gốc và đỉnh lá là ngoại lệ của tính chất trên, với đỉnh gốc không có cha, đỉnh lá không có con.
• Đỉnh có khoảng cách tới gốc ngắn hơn sẽ là tổ tiên (ancestor) của đỉnh có khoảng cách tới gốc xa hơn. Ngược lại, đỉnh xa hơn sẽ là hậu duệ (descendant) của đỉnh gần hơn.
• Tổ tiên thứ k (Kth-ancestor) của một đỉnh u là một đỉnh v có hậu duệ là đỉnh u và khoảng cách của 2 đỉnh đúng bằng k.

4. Khoảng cách từ gốc đến một đỉnh được gọi là chiều cao (height) hoặc chiều sâu (depth) của đỉnh. Chiều cao của cây T là giá trị của đỉnh có chiều cao lớn nhất.

5. Đường kính (diameter) của cây T là khoảng cách lớn nhất giữa hai đỉnh trong cây.

Có 3 cách phổ biến để biểu diễn đồ thị trong chương trình: ma trận kề, danh sách kề và danh sách cạnh. Tùy theo đề bài mà ta sẽ áp dụng các cách lưu trữ khác nhau.

Ta giả sử dữ liệu nhập của một đồ thị là một danh sách cạnh.

Đồ thị ví dụ:

Ma trận kề là một cấu trúc đơn giản được dùng để lưu một đồ thị bất kì.

Để biểu diễn đồ thị G(V, E) trong ma trận kề, ta xây dựng ma trận vuông A với:

• A[u][v] = 1 nếu uv \in E(G)
• A[u][v] = 0 nếu uv \notin E(G)

Ngoài ra:

• Nếu đồ thị có trọng số, ta thay 1 bằng trọng số của cạnh tương ứng.
• Nếu đồ thị vô hướng, ta đánh dấu cả A[x][y] và A[y][x], còn nếu có hướng thì chỉ đánh dấu A[x][y].

const int N = 1010; 
int n, m;
int mat[N][N];
int main() {
	cin >> n >> m;
	for(int i = 0; i < m; ++i){
		int a, b; cin >> a >> b;
		mat[a][b] = 1; // Nếu đồ thị có trọng số thì đổi 1 thành w
		mat[b][a] = 1; // Nếu đồ thị có hướng thì không cần viết dòng này
	}
	return 0;
}

Danh sách kề là cách lưu trữ đồ thị phổ biến trong lập trình thi đấu. Để biểu diễn đồ thị bằng danh sách kề, ta tạo N mảng giá trị, mảng giá trị thứ u lưu danh sách các đỉnh kề với đỉnh u.

const int N = 1e5 + 10; 
int n, m;
vector<int> adj[N];
int main() {
	cin >> n >> m;
	for(int i = 0; i < m; ++i){
		int a, b; cin >> a >> b;
		adj[a].push_back(b); 
		adj[b].push_back(a); // Nếu đồ thị có hướng thì không cần viết dòng này
	}
	return 0;
}

Nếu đồ thị có trọng số thì với mỗi cạnh (a, b) có trọng số w, ta lưu cặp giá trị (b, w) trong adj[a]. Có thể lưu cặp giá trị (b, w) bằng kiểu dữ liệu pair.

vector<pair<int, int>> adj[N];
adj[1].push_back({2, 3}); // lưu cạnh (1, 2) có trọng số 3

Danh sách cạnh được dùng để lưu các cạnh trong đồ thị.

Ta có thể lưu các cạnh của đồ thị bằng pair hoặc tạo một cấu trúc struct tùy ý để lưu cặp giá trị có trong cạnh của đồ thị.

struct Edge{
	int a, b, w; // w được dùng cho đồ thị có trọng số
	Edge(int u, int v, int weight): a(u), b(v), w(weight){}
	bool operator<(const Edge &e) const{
		return w < e.w; // Sắp xếp theo trọng số các cạnh
	}
};

int main() {
	int n, m; cin >> n >> m;
	vector<Edge> edges;
	for(int i = 0; i < m; ++i){
		int a, b, w; cin >> a >> b >> w;
		edges.push_back(Edge(a, b, w));
	}
	return 0;
}